My last post, on March 30th, argued for physical modelling of the spread of the pandemic that still continues to dominate our daily lives. I also argued for a universal profile for the pandemic growth, starting with a super-exponential growth at early times (as a superposition of many infection clusters), followed by saturation and decay.
In particular, the best-fit “universal model” to Italy, US, and Canada (on March 29th) predicted that: “… Canadian mortality will pass 1000 around April 9th, while the US mortality will pass 10,000 around April 5th.”
As you can see below, while the latter milestone did indeed come to pass, the Canadian rate has fortunately slowed down since the end of March, and we are so far below 1000 COVID-19 fatalities in Canada.

In fact, exactly how the spread of a contagion slows down was beyond the scope of my last post, but clearly it is what we care about the most as a society. So, given the wealth of data that is available on the spread of COVID-19 across the world, I decided to figure out how the data can tell us when a slow-down might be happening.
There are different ways that different outlets decide to visualize this. Probably one of the better ones is the number of daily confirmed fatalities as a function of time:

While this is a good measure, it still has a few caveats. One obvious caveat is that there could be many deaths that were missed, especially at peaks of outbreaks (e.g., due to death at home), or misidentification of the cause of death. Another caveat is that it is hard to compare different countries, due to their different populations, or different sizes of outbreaks.
A New Measure
To solve the latter problem, I will now introduce the Relative Daily Increase in Reported Death, , which is defined as:

where is the number of daily confirmed death, on day
. For example,
implies that the number of reported deaths today, is
% higher than the number of reported deaths yesterday. To reduce the scatter, I will actually use a rolling average over 14 days, i.e.

For example, /day today means that the number of reported death in the past 7 days (including today) were twice (
) that of the preceding 7 days.
Of course, what we really need is this number for the infected individuals, but given the arbitrariness and shortcomings in testings across municipalities, and the prevalence of asymptomatic individuals, I think the mortality numbers (even with all its shortcomings) may give a more reliable measure of the epidemic. However, there is clearly a time-delay between the exposure and death, which needs to be taken into account if one wants to relate the mortality statistics to the epidemic dynamics. According to current clinical studies, the incubation period (the period from exposure to onset of symptoms) is 4 to 7 days , while the time from onset of symptoms to death (on average) is 17 to 19 days (both at 95% confidence level). Given my lack of knowledge of how these uncertainties may be correlated, I take the conservative range of 21-26 days, as the expected time delay from exposure to death. Now, since depends on mortality data in the past 14 days, the 21-26 day delay implies that it takes at least 21 days for any effect of, e.g., social distancing to show up in
, but it may take up to 14+26=40 days to see the full effect.
United States vs. Canada: Comparison of COVID-19 Mortality Growth Rates
So, after all this introduction, the next plot compares between the United States and Canada, where the errorbars are simple Poisson errors.

As I had predicted in my last post, both US and Canada show an early rise in death growth rates, which could be attributed to different competing epidemic clusters. Since US is more geographically diverse, it has a faster rise. However, they both reach a peak, US around March 25th, and Canada around April 9th, following which the rates start to drop precipitously. In fact, it appears that daily death rates might have peaked for both countries in the last couple of days, i.e.
, although it may take a few days for it to show up in
(if it is indeed real, and not a statistical fluke).
But what is responsible for these precipitous drops in mortality growth rates? The natural response might be that preventative measures, such as lockdowns and social distancing have started to work. To test this hypothesis, we can compare the recently released mobility data from Google, that shows how lockdowns have affected the two countries (I only show the first row of the report, which is representative of the drop in other social activities) .

We notice that the activities in both countries start to drop around March 15th, and take almost a week to reach their plateau. If this drop can mitigate the spread of COVID-19, given the 21-day delay that we discussed above, it should only start to affect the mortality after April 5th, which could well fit the rapid drop in Canadian mortality growth (or ), on April 9th. But what about the US, whose mortality growth peaked on March 25th? For that, the spread of the virus must have slowed down well before March 4th. Even looking at the mobility reports for Washington and New York States, which are respectively the earliest and the biggest US epicenters of the pandemic, show little change in social activities prior to March 8th. More curiously, even though US and Canada started their social distancing around March 15th (even though US’s -49% is not quite as impressive as Canada’s -63%), the precipitous drop in Canadian mortality rate around April 9th, has no counterpart in US’s data (in spite of its much smaller Poisson errors).
Mystery Deepens
To understand how unique the situation with the US might (or might not) be, I decided to compare it to mortality growth rate, , for other countries. In the next plot, I am comparing this measure for the 9 countries with the highest reported total death (I am excluding Iran here, as its official figures might be a significant underestimate). I have shifted all the curves, so that their peak is at
.
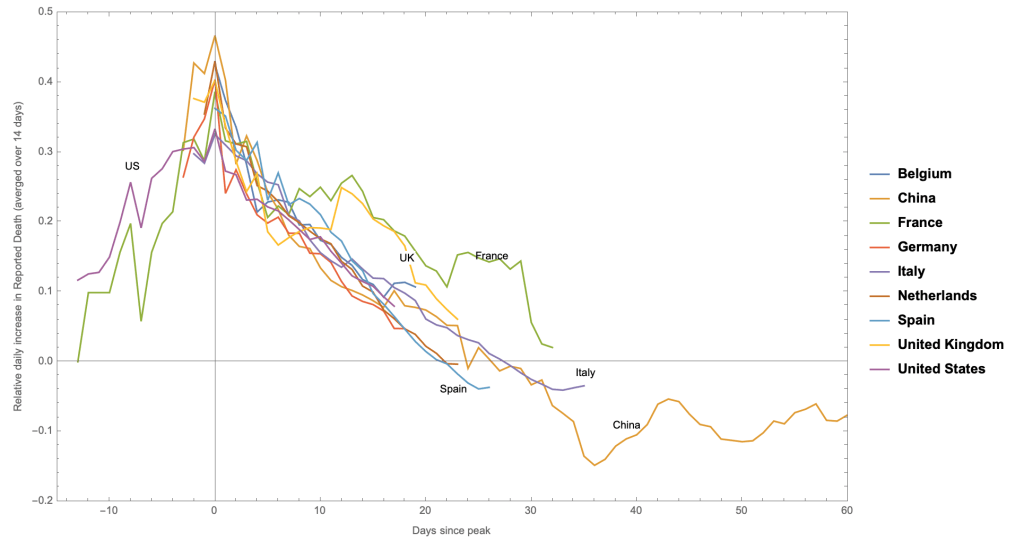
Most countries (with the exception of US and France), don’t have much data prior to the peak. This could well be because the epidemic was growing in the dark and under the radar (as it is believed was the case, e.g. in Italy).
More interestingly, it also appears that the mortality growth rates falls precipitously, in essentially an identical fashion to the US, past the peak: They all appear to peak around /day (at 1-
), and linearly decrease, with similar slopes that cross zero (i.e. max. daily death) within 21-27 days. The two exceptions are the UK and France that appear to undergo secondary and tertiary outbreaks.
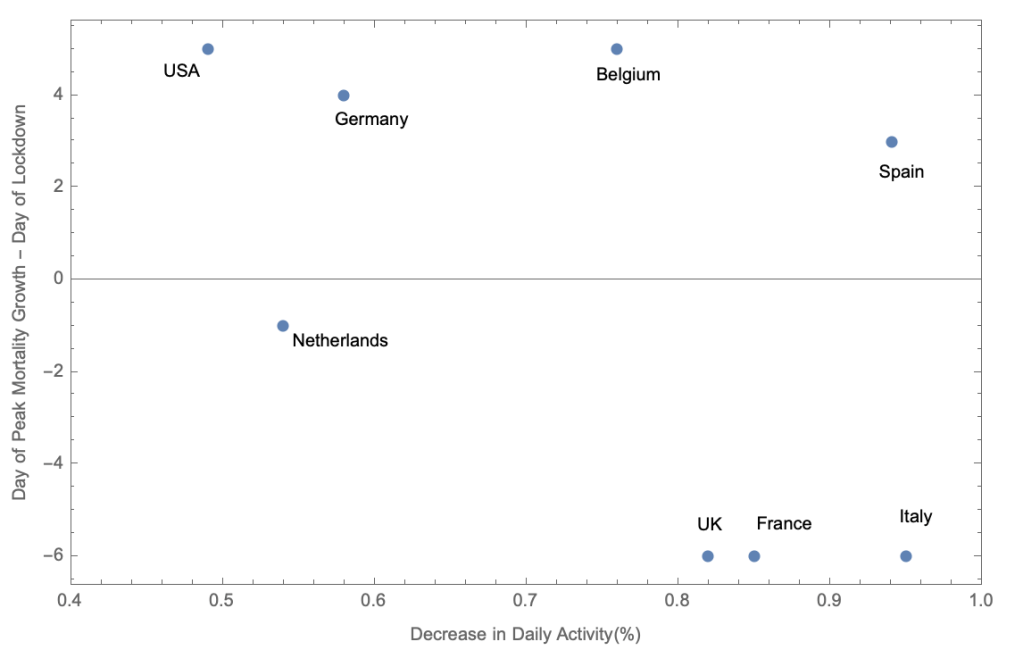
Similar to the US, there appears to be no correlation between the dates of the lockdown (defined as when the social mobility plateaus to its lockdown rate) , and those of the peak mortality rate , no matter how effective the lockdown has been.
“Herd Immunity” vs Lockdown
There is an interesting coincidence between the numbers that we discussed above. The 21-27 days from the peak of to when it crosses zero (i.e. max. daily fatality), which is common amongst the 9 countries with biggest total death (excluding Iran) is identical to the 21-26 days exposure-to-death period, inferred for COVID-19. Therefore, if we are near the peak of the epidemic with
/day, i.e. twice as many people are infected tomorrow as they were yesterday, and you suddenly stop the infections today, then most fatalities will happen 21-26 days from today. This would explain the universality of the universal precipitous drop in
.
But what would suddenly stop the spread at the peak? As the last plot showed, there doesn’t seem to be an obvious causal relationship between the lockdown and the peak in mortality growth. In fact, one may speculate that the lockdown might be more of a sociological response to large mortality growth. To shed light on this situation, let’s make a comparison between four countries, Canada and Austria (with more effective lockdown starting at small ), USA (with less effective lockdown starting at already large
) and Sweden (with no effective lockdown):

We see that, for Austria and Canada, as we argued above, the rapid drop and small peak at , is a likely (and timely) response to social distancing measures. However, countries with late or no lockdown will reach a universal maximum, until they presumably reach some version of “herd immunity”, at which point the death rate drops in a universal fashion (case in point: US and Sweden curves are indistinguishable beyond the peak, despite vastly different populations). The problem with “herd immunity”, however, is that it may need to happen over and over again, within different communities in a country, as it seems to be happening in France and the UK.
Bottom Line
At this point, if you managed to make it this far (congratulations by the way! you are excellent at extreme social distancing👏), you may have hoped to find one concise conclusion. I am afraid to disappoint you!
I guess one lesson might be that you may always learn new things by plotting different statistical measures of a physical phenomenon, including a pandemic. I also think the universal behavior of mortality growth rate, as I have defined here, at least with countries with large number of deaths was a surprise to me, and something that I hadn’t seen anywhere else. I also believe the existence of a dark onset of epidemic for most countries in Europe and China (having missed the early rise), might be another lesson from these plots. As to the most important question, i.e. the role of “herd immunity” vs. “lockdown”, it appears hard to distinguish the two possibilities, as they both appear to happen around the peaks of a pandemic in a community. However, countries with poorer and/or later lockdowns appear to see higher peaks and/or slower decays of the mortality growth rate (translating to a larger overall fatality per capita). Ultimately though, this is intimately related to the prevalence of asymptomatic and undetected spreaders, the more of them around, the less fatal is COVID-19 and we reach “herd immunity” faster, while an effective lockdown and contact tracing will become harder.
In the end, let me thank Ghazal Geshnizjani, Ben Holder and Bruce Bassett for many useful discussions. In particular, Bruce has some excellent analysis on data science with COVID-19 that can be found on his Linked-In Page.
Update (April 14th, at 9:12am EDT): The last figure was updated to include Austria (a similar sized country to Sweden), as was suggested by Ghazal Geshnizjani.


[…] we looked at 14-day average of daily mortality growth rate, i.e. the exponent of the exponential growth rate as a pan-epidemic, dynamical, measure of […]
LikeLike